Elean Zeno on kreikkalainen logistiikka ja filosofi, joka tunnetaan lähinnä hänen kunniakseen nimetyistä paradokseista. Hänen elämästään ei tiedetä paljon. Kotikaupunki Zeno on Elea. Myös Platonin kirjoituksissa mainittiin filosofin tapaaminen Sokratesin kanssa.
Noin 465 eaa e. Zeno kirjoitti kirjan, jossa hän esitteli kaikki ideansa. Mutta valitettavasti se ei ole saavuttanut aikamme. Legendan mukaan filosofi kuoli taistelussa tyrannin (oletettavasti Elea Nearchin pään) kanssa. Kaikki tiedot Eleasta kerättiin vähitellen: Platonin (syntynyt 60 vuotta myöhemmin Zeno), Aristoteleen ja Diogenes Laertiuksen teoksista, jotka kirjoittivat kolme vuosisataa myöhemmin kreikkalaisten filosofien elämäkerhojen kirjan. Zenoa mainitaan myös kreikkalaisen filosofian koulun myöhempien edustajien kirjoituksissa: temistia (4. vuosisadan luvu), Alexander Afrodinsky (3. vuosisadan lujuus) sekä Philoponus ja Simplicius (molemmat asuivat 6. vuosisadan luona).. Lisäksi näiden lähteiden tiedot ovat niin johdonmukaisia, että on mahdollista rekonstruoida kaikki filosofin ajatukset. Tässä artikkelissa kerrotaan sinulle Zenon paradokseista. Joten aloitetaan.

Sarjan paradoksit
Pythagoran aikakaudesta lähtien tilaa ja aikaa tarkasteltiin yksinomaan matematiikan näkökulmasta. Toisin sanoen niiden uskottiin koostuvan monista kohdista ja kohdista. Heillä on kuitenkin ominaisuus, joka on helpompi ymmärtää kuin määritellä, nimittäin ”jatkuvuus”. Jotkut Zeno-paradoksidit todistavat, että sitä ei voida jakaa hetkiin tai pisteisiin. Filosofin päättely laskee seuraavaan: ”Oletetaan, että olemme suorittaneet jaon loppuun saakka. Silloin vain yksi kahdesta vaihtoehdosta on totta: joko saamme pienimmät mahdolliset määrät tai osia, jotka ovat jakamattomia, mutta määrää äärettömiä, tai jako johtaa meidät osiin ilman suuruutta, koska jatkuvuuden, joka on homogeenista, on oltava jaettavissa kaikissa olosuhteissa.. Sitä ei voida jakaa toisessa osassa, mutta toisessa ei. Valitettavasti molemmat tulokset ovat melko naurettavia. Ensimmäinen johtuu siitä, että jakamisprosessi ei voi päättyä, kun taas jäljellä olevissa osissa on arvo. Ja toinen johtuu siitä, että tällaisessa tilanteessa alun perin kokonaisuus olisi muodostettu tyhjästä. ” Simplicius katsoi tämän argumentin Parmenidesille, mutta on todennäköisempää, että sen kirjoittaja on Zeno. Menemme pidemmälle.
Zenon liikkeen paradoksit
Niitä pidetään useimmissa filosofille omistetuissa kirjoissa, koska ne joutuvat dissonanssiin todisteiden kanssa eleattisten tunteista. Suhteessa liikkeeseen erotetaan seuraavat Zeno-paradoksidit: “Arrow”, “Dichotomy”, “Achilles” ja “Stages”. Ja he tulivat meille Aristoteleen ansiosta. Katsotaanpa niitä lähemmin.
"Arrow"
Toinen nimi on Zenon kvanttiparadoksi. Filosofi väittää, että mikä tahansa asia joko seisoo tai liikkuu. Mutta mikään ei ole liikkeessä, jos miehitetty tila on yhtä pitkä sen kanssa. Tietyllä hetkellä liikkuva nuoli on yhdessä paikassa. Siksi se ei liiku. Simplicius muotoili tämän paradoksin lyhyessä muodossa: ”Lentävä esine vie yhtä suuren paikan avaruudessa, mutta se, joka vie saman aseman avaruudessa, ei liiku. Siksi nuoli on levossa. ” Femistius ja Phelopon muotoilivat samanlaisia vaihtoehtoja.
"Dichotomy"
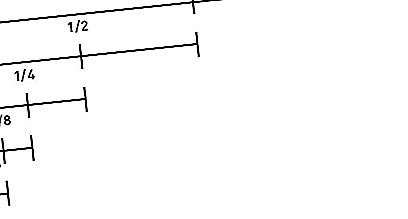
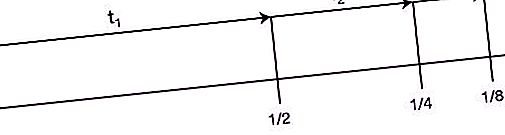
Ottaa toisen sijan "Zeno Paradoxes" -luettelossa. Se kuuluu seuraavasti: ”Ennen kuin liikkuva esine voi kulkea tietyn matkan, sen on ylitettävä puolet tästä polusta, sitten puolet jäljellä olevasta jne. Äärettömyyteen. Koska etäisyyden toistuvien jakamisten aikana puoliksi, segmentistä tulee jatkuvasti äärellinen ja näiden segmenttien lukumäärä on ääretön, tätä etäisyyttä ei voida ylittää rajallisessa ajassa. Lisäksi tämä väite on totta sekä pienillä etäisyyksillä että suurilla nopeuksilla. Siksi kaikki liikkeet ovat mahdottomia. Toisin sanoen juoksija ei edes voi aloittaa."
Tämä paradoksi kommentoi yksityiskohtaisesti Simpliciusta osoittaen, että tässä tapauksessa on tehtävä ääretön määrä kosketuksia rajallisessa ajassa. "Jokainen, joka koskettaa jotain, voi laskea, mutta ääretöntä joukkoa ei voida selvittää tai laskea." Tai kuten Philopon totesi, ääretön joukko on määrittelemätön.
"Achilles"
Tunnetaan myös nimellä Zeno-kilpikonnan paradoksi. Tämä on suosituin filosofinen peruste. Tässä liikkumisen paradoksissa Achilleus kilpailee kilpikonnalla, jolla on alussa pieni haitta. Paradoksi on, että kreikkalainen soturi ei kykene kiinni kilpikonnaan, koska ensin hän saavuttaa sen lähtöpaikan ja hän on jo seuraavassa pisteessä. Toisin sanoen kilpikonna on aina Achilleuksen edessä.
Tämä paradoksi on hyvin samanlainen kuin kaksijakoisuus, mutta tässä ääretön jako kulkee etenemisen mukaan. Kaksitahoisuuden tapauksessa tapahtui regressio. Esimerkiksi sama juoksija ei voi aloittaa, koska hän ei voi poistua sijainnistaan. Ja akilles-tilanteessa, vaikka juoksija alkaa liikkua, hän ei silti tule juoksemaan minnekään.
"Flock"
Jos vertaamme kaikkia Zenon paradokseja monimutkaisuuden suhteen, se olisi voittaja. Se on vaikeampaa kuin toiset selittää. Simplicius ja Aristoteles kuvasivat tätä päättelyä hajanaisesti, eikä sen luotettavuuteen voida luottaa 100-prosenttisesti varmuudella. Tämän paradoksin rekonstruoinnilla on seuraava muoto: olkoot A1, A2, A3 ja A4 samansuuruiset liikkumattomat rungot ja B1, B2, B3 ja B4 ovat samankokoisia kappaleita kuin A. B-rungot liikkuvat oikealle siten, että jokainen B kulkee Ja yhdessä hetkessä, joka on pienin ajanjakso kaikista mahdollisista. Olkoon B1, B2, B3 ja B4 samanlaisia kappaleita kuin A ja B ja liikkuvat suhteessa A vasemmalle, ylittäen jokaisen ruumiin yhdellä hetkellä.
On selvää, että B1 voitti kaikki neljä B: n ruumista. Otetaanpa yksikköä varten aika, joka kului yhden B-kappaleen kuljettamiseen yhden B-kappaleen läpi. Tässä tapauksessa tarvitaan neljä yksikköä kaikkeen liikkeeseen. Uskottiin kuitenkin, että kaksi hetkeä, jotka kulkivat tälle liikkeelle, olivat minimaaliset ja siksi jakamattomat. Tästä seuraa, että neljä jakamatonta yksikköä on yhtä suuri kuin kaksi jakamatonta yksikköä.